World-Space Normal Mapping

Le normal mapping est une technique de rendu permettant d'augmenter la complexité d'une scène sans augmenter le nombre de polygones. Comme la plupart des techniques, il s'agit d'une illusion : ainsi une surface pourtant plane apparaitra bosselée au joueur grâce à un éclairage plus détaillé.

Coefficient Lambert

En 3D, lorsqu'on détermine l'éclairage d'un point, on a besoin d'une normale. Cette normale est utilisée pour calculer le "coefficient Lambert", soit l'intensité de la lumière en un point.Soient N la normale, L la direction de la lumière et E celle de la caméra :

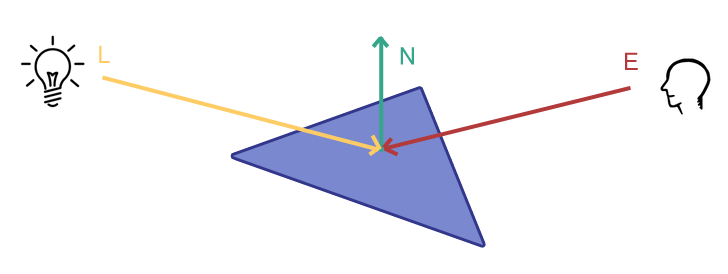
Le coefficient nous est donné via : c float lambert = max ( 0 , dot ( N, -L ) );

Et de façon similaire, pour la lumière spéculaire:

c float specular = pow ( saturate ( dot ( normalize ( E - L ) , N ) ) , specularPower );

C'est ce que les cartes graphiques faisaient depuis la nuit des temps, avec leurs Fixed-Function Pipelines. Malheureusement, les normales d'un triangle sont définies à chaque sommet (vertex) puis interpolées pour chaque pixel. Par conséquent, la surface d'un triangle est définie, dans le meilleur des cas, par trois normales.

L'idée du normal mapping, c'est de définir des normales spécifiques pour chaque point du triangle. Pour prendre un exemple, voici une scène éclairée avec les normales indiquées par chaque vertex :

Normal maps

Pour cela on va avoir recours à des "normal maps" : des textures appliquées à nos modèles qui vont "plaquer" une normale spécifique à chaque point. Les normales étant des vecteurs normalisés, on peut facilement les représenter via des couleurs. R = X, G = Y et B = Z.

Ces normal maps sont réalisées par les artistes, soit en les dessinant à la main (difficile), soit en les générant à partir d'une texture diffuse déjà existante (approximatif) soit en "bakant" un modèle haute-définition sur une texture (la technique la plus commune). C'est tout l'intérêt d'un logiciel comme Z-Brush qui permet de sculpter un modèle existant pour ajouter des détails et les exporter ensuite sous forme de normal map.

A ce stade, je pense que vous voyez où je veux en venir : on va passer cette normal map à notre pixel shader et calculer le coefficient Lambert directement pour chaque pixel ("per-pixel lightning"), plutôt que pour chaque sommet.

Sauf que c'est pas aussi simple.

Tangent Space

Si vous cherchez des exemples de normal maps sur le net, vous verrez une prédominance de bleu clair :

C'est parce que les normales sont représentées dans ce qu'on appelle l'espace tangent ("tangent space").

Imaginez que vous souhaitiez ajouter une normal map au sol : vos normales vont tendre vers +Y (prédominance de vert). Mais si vous voulez plaquer une normal map sur un mur, ce sera du +X, ou du +Z. Ou même du -X ou du -Z ! Vous n'allez pas réaliser une variation de chaque normal map pour toutes les configurations et angles possibles, pas vrai ? Et si votre modèle tourne ?

L'espace tangent nous permet de décrire nos normales de façon unifiée.

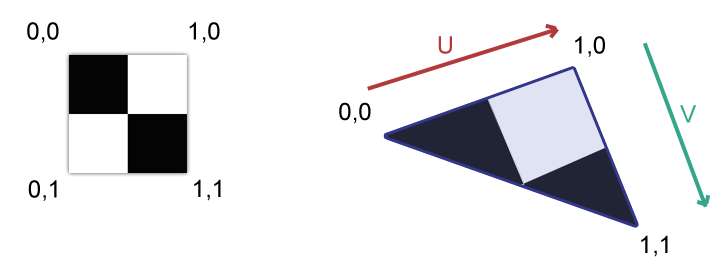
En théorie, la définition de cet espace est simple : il est formé sur la surface du triangle ("perpendiculaire" à la normale), suivant les axes U et V qu'on utilise déjà pour nos coordonnées de texture.

Matrice TBN

A ce stade-là, on a deux possibilités :

• Convertir nos vecteurs L et E vers l'espace tangent ("tangent-space normal mapping")
• Convertir notre normale N vers l'espace monde ("world-space normal mapping")

Pour cet article, on va privilégier la seconde méthode, car elle a l'avantage d'être plus simple à débugger : vous pouvez afficher les normales avec le pixel shader pour vous rendre compte de si elles sont bonnes ou non. Avec le tangent-space normal mapping... c'est plus obscur.

Pour transformer une normale exprimée dans l'espace tangent vers notre espace monde, on va avoir besoin d'une matrice, souvent nommée "TBN" pour "Tangent, Bitangent, Normal".

(Vous trouverez souvent le mot "Binormal" au lieu de "Bitangent" : c'est une erreur. Comme les nattes inversées des lecteurs disquettes : quelqu'un s'est planté au tout début et le mauvais usage survit.)

Si la normale N forme l'un des axes de notre espace tangent, les vecteurs "Tangent" et "Bitangent" (T et B) sont les deux autres. Ils sont dérivés de U et V (des vecteurs 2D).

Du coup pour obtenir notre matrice TBN, il va nous falloir récupérer les vecteurs T et B pour chaque vertex, en plus du N qu'on a déjà. Certains combos de logiciels de modélisation et de formats vous permettront d'exporter ces vecteurs, mais il existe des techniques pour les calculer.

L'une d'elles est la méthode de Lengyel pour calculer T. Voici un exemple d'implémentation.

Ce vecteur T va devoir suivre N dans notre vertex definition :

c struct VSInput { float4 Position : POSITION0; float2 TexCoord : TEXCOORD0; float3 Normal : NORMAL0; float4 Tangent : TANGENT; float4 Color : COLOR0; };

Une fois que l'on a T et N, on peut déterminer B, directement dans le vertex shader :

c float3 B = cross( N , T.xyz ) * T.w;

Et la matrice TBN :

c float3x3 tbn; tbn[0] = normalize ( mul ( xWorld , float4(T,0) ).xyz ); tbn[1] = normalize ( mul ( xWorld , float4(B,0) ).xyz ); tbn[2] = normalize ( mul ( xWorld , float4(N,0) ).xyz );

Qu'on passera à notre pixel shader.

Lumière !

Dans le pixel shader, on peut multiplier la couleur obtenue par la normal map avec notre matrice TBN pour obtenir la normale dans l'espace monde :

c float3 normal = normalize(2.0 * tex2D ( NormalsSampler , input.TexCoord ).xyz - 1.0); normal = mul ( normal , input.TBN );

Vous noterez le "*2 - 1" qui permet de passer du spectre [0,1] offert par le RGB au [-1,1] que l'on souhaite.

Si on décide d'afficher nos normales, ça devrait donner ça :

Notez que les surfaces pointant vers le haut sont vertes, celles vers +X sont rouges, +Z donne du bleu et -X et -Z donnent du noir (puisque < 0).

Ça veut dire que ça marche !

Il ne nous reste plus qu'à reprendre notre formule pour calculer les coefficients lambert et spéculaire et éclairer notre scène comme on l'entend :

Et voilà !